El valor esperado o esperanza matemática, en inglés “expected value”, de ahí sus siglas EV, es el cálculo más valioso que un apostante de mercados medianamente líquidos puede hacer para conocer el nivel de sus apuestas. En mi opinión, es la única forma para saber si vamos por el buen camino. Todo ello, a pesar de que el EV en apuestas nunca va a ser tan exacto como en póker u otros juegos con la probabilidad conocida.

Antes de nada, es preciso diferenciar los mercados de apuestas reales, donde las cuotas vienen marcadas por el equilibrio fijado por los apostantes y donde hay facilidad para poder apostar en el intercambio, de los desajustes de las casas de apuestas, que son esos mercados secundarios con grandes errores de colocación de cuotas, sin mercado de equilibrio, y donde los más rápidos con cuentas "no limitadas" pueden sacar provecho. De hecho, es a través de este segundo modelo de apuestas por el que son ganadores la gran mayoría de apostantes. Quiero aclarar que para este tipo de apuestas, lo que voy a tratar de explicar en las siguientes líneas, no sirve, al no existir un mercado propiamente dicho.

Juegos de casino, póker y apuestas

Todos los juegos de casino, donde el jugador juega directamente contra la banca tienen un EV negativo para los jugadores, que juegan a juegos donde la probabilidad es conocida y con una desventaja con respecto a la casa. Es inevitable por ello, que todos los jugadores de Casino acaben perdiendo dinero en el tiempo si se convierten en asiduos.

En el caso del póker, todo jugador puede saber con certeza, una vez se muestran las cartas, en qué porcentaje de ocasiones ganaría esa mano, para tener la seguridad de que está teniendo buena o mala suerte. Esta es la mayor ventaja que considero que posee el póker respecto a las apuestas, la probabilidad conocida una vez se muestran las cartas.

Para explicar todo esto voy a tratar de exponer un caso sencillo de apuestas deportivas donde la probabilidad es conocida.

Pongamos el clásico ejemplo de la moneda donde la casa de apuestas paga 1.90 que salga “cara” y 1.90 que salga “cruz” en el saque inicial de un gran evento. Con esos datos, ya podemos saber el payout (más info haciendo click) utilizando la fórmula. La recordamos.

(1/Cuota A) + (1/Cuota B) = R

Porcentaje de Payout = (1/R) x 100

En nuestro caso 0,5263 + 0.5263 = 1.052

Payout = 1/1,052 = 0.95 (95%)

Una vez conocido el payout podemos proceder a conocer cual es nuestro valor esperado (EV) apostando a “cara” con la siguiente fórmula:

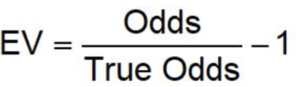
Para ello necesitamos conocer dos datos, las “Odds” que serían las cuotas a las que apostamos y las “True Odds” que serían las cuotas reales restando la comisión de la casa. Tratándose de una moneda conocemos con exactitud la probabilidad, que será 50%, y por tanto la cuota real será 2. Lo vemos con la fórmula.

True Odd = Odd/Payout

En nuestro caso, True Odd = 1.90/0.95 = 2

Por tanto EV = (1.90/2.00) -1 = -0.05 (-5%)

Esto significa que estamos apostando con un valor esperado negativo del 5%, lo que significa que perderemos el 5% de todo lo apostado en el tiempo.

¿Y cómo podemos saber esto para el resultado de un partido?

Efectivamente, tal y cómo imagináis, la probabilidad no la podemos conocer con certeza, sin embargo, por numerosos estudios, lo que sí sabemos es que los precios más efectivos son los de cierre, esto es, los que existen justo en el momento que arranca el partido. Por ello, el cálculo del EV, dando como buena esta cuota -aun sabiendo que no existe nunca la total certeza- será nuestra referencia y la referencia de los grandes apostantes para no caer en la famosa "ilusión de la habilidad" (más info haciendo click).

El objetivo de todo pronosticador ha de ser conseguir un valor esperado positivo o esperanza matemática positiva, denominada con las siglas EV+ y escapar del EV- tal y como pasaba en el ejemplo de la moneda o en cualquier juego de casino. Y ello es posible porque las cuotas fluctúan desde su salida hasta el momento del pitido inicial.

Para mostrar el funcionamiento, os dejo el ejemplo de un muy buen pick de febrero que además salió ganador. Se trata del "Sevilla +0.5 AH" en el partido "Valencia-Sevilla" del pasado 17/02/24 hecho y publicado a 1.82 con cierre a 1.69. En la imagen de oddsportal podéis ver ya directamente el payout a cierre, sin la necesidad de calcularlo.

Procedemos como en el ejemplo de la moneda, dando como probabilidad real la de cierre. Reitero, la probabilidad real nunca se va a conocer, pero lo que si sabemos a grandes números es que la de cierre es la que más se acerca a la realidad y por tanto, es nuestra guía para sobrevivir.

True Odd = Odd/Payout donde, "cuota real o true odd" es la cuota de cierre una vez restada la comisión y "cuota u odd" es la cuota que llevamos nosotros (1.82).

La cuota de cierre es 1.69, sin embargo, el payout es 97.6% l cual significa que la cuota real es un poco más alta. Debemos restarle la comisión que es tan sencillo como dividir la cuota entre el payout en tanto por uno. Esto es 1.69/0.976 = 1.731 , esta será la cuota real de cierre por lo que ya tenemos todo.

En nuestro caso, por tanto , True Odd = 1.69/0.976 = 1.731

Por tanto EV = (1.82/1.731) -1 = 0.0514, que si lo pasamos a tanto por ciento nos sale 5.14.

Esto significa que estamos apostando con un valor esperado positivo (EV+) del 5.14%, que es mucho tratándose de una línea principal de salida en un mercado principal de Primera División.

Si haces esto con todos tus pronósticos en líneas principales, podrás tener una referencia muy importante para saber como estás leyendo la temporada, y cuantas más temporadas lleves, más referencias tendrás para sacar tus propias conclusiones y ver donde puedes mejorar y donde lo estás haciendo mejor.

Para acabar, es importante añadir que el margen de la casa de apuestas depende del nivel de cuotas, a más precio, más margen de las casas y viceversa. Esto es algo que no afecta en líneas principales pero que es preciso comentar.